애니메이션 easing에 숨은 비밀

UI 애니메이션을 코딩할 때 꼭 들어가는 양념 같은 게 있다. easing. 우리 말로는 한 마디로 옮기기 힘들어 풀어서 말하자면 애니메이션 흐름을 매끄럽게 이어주기 위해 동작 속도를 조절하는 것이다. (경제 용어에서는 quantitative easing을 "양적 완화"로 옮기기는 한다.)

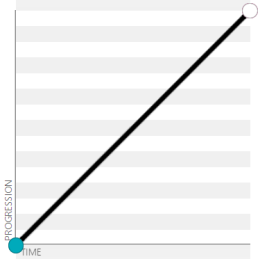
이미 아는 사람은 알겠지만 예를 들자면 easing이 없다면 이러던 것이,

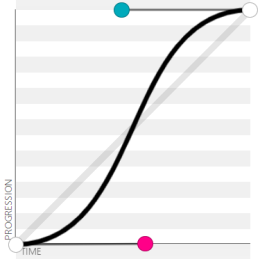
아래처럼 매끄럽고 자연스러운 느낌의 움직임으로 바뀐다.

전자는 시작과 끝에서 뭔가 뚝 끊기는 느낌이 드는데 후자는 자연스럽게 시작하고 끝난다. 그리고 두 애니메이션에 걸리는 시간은 동일하다! 차이는 전자는 일정 속도로 움직이는 것이고 후자는 처음과 끝에는 속도를 낮추고 중간에는 속도를 빨리하는 데 있다. 아래는 그러한 움직임을 그래프로 나타낸 것이다. 운동 속도 = (움직인 거리 / 시간), 즉 $v = \dfrac{\Delta s}{\Delta t}$이므로 그래프의 기울기가 속도다. 기울기가 큰 곳은 빠르고 완만한 곳은 느린 부분이 되겠다.

(혹시 소스가 필요하다면 이 페이지의 소스 보기를 확인하도록.)

easing이 들어간 편이 좀더 매끄럽게 느껴지는 이유는 사람이 속도에는 둔감해도 가속도에는 민감하기 때문에 그렇다. 위 두 가지 예에서 전자는 처음과 끝에서 무한대 크기의 가속도가 발생하는데 반해 후자는 가속도가 서서히 높아졌다가 낮아지게 된다. (가속도는 속도의 기울기이므로 위 그래프에서 유추해보자~ 😉 )

일상 생활에서는 우리가 가속도를 따지는 일이 별로 없지만(자동차가 100m/s까지 도달하는 데 몇 초가 걸리는지 따지는 정도?) 실제로는 사람이 교통 수단이나 놀이기구를 탄다든가 연장을 쓰거나 힘을 쓸 때 얼마나 매끄럽게 움직이냐, 얼마나 빨리 떨어지냐, 얼마나 힘이 잘 먹히냐 등의 기준이 되는 것이 바로 가속도다. 혹시 뉴턴의 그 유명한 운동의 법칙을 기억한다면 알 수 있는 $F = ma$을 통해서 본다면 가속도는 곧 힘이기 때문이다.

속도에는 둔감하고 가속도에는 민감한 예를 들자면 차가 일정한 속도로 달리고 있을 때 우리는 이 차가 얼마나 빨리 움직이는 것인지 잘 모른다. 일정한 속도라면(즉, 가속도가 0이라면) 차안에서 가만히 서있을 수 있다. 하지만 급정거나 급출발하면 어떤가? 아무리 살짝(?) 급정거, 급출발을 해도 우리는 곧바로 느낄 수 있다. 우리 몸이 힘을 맞았기 때문이다.

UI 애니메이션에서 easing은 이런 가속도를 매끄럽게 해주는 일을 한다. 위 이동 그래프에 나타난 것과 같이 이동 그래프의 선이 얼마나 매끄럽게 이어지느냐가 바로 매끄러운 움직임을 나타내는 것이라고 보면 된다. 갑자기 꺾이거나 튀는 부분이 바로 가속도가 튀는 부분이고 이런 게 움직임을 자연스럽지 못하게 만든다.

사실 공학(engineering)이라는 것의 상당 부분이 이런 easing과 같은 문제가 얽혀 있다고 볼 수 있다. 똑같은 기능이라도 잘 팔리는 물건은 말하자면 미세한 부분이 다르다. 그 미세한 부분이 바로 easing과 같이 사람의 느낌이나 감성을 건드리는 부분인 것이다. 또한 거기에 인문학이 더해지면 품격까지 높은 물건이 만들어진다고 한다. 엉뚱한 얘기일 수도 있지만 easing 곡선 하나를 만드는 데도 중세의 건축 양식에 있는 곡선을 적용한다면 사람들은 그걸 느낀다는 거다. 정말이라고. 사람들이 얼마나 예민한데!